Теоретический материал к задаче B8
Производная функции в точке — основное понятие дифференциального исчисления,
характеризующее скорость изменения функции (в данной точке). Определяется как
предел
отношения приращения функции к приращению ее аргумента при стремлении
приращения
аргумента к нулю, если таковой предел существует. Функцию, имеющую
производную
(в некоторой точке), называют дифференцируемой (в данной точке). Процесс
вычисления производной
называется дифференцированием.
Геометрический смысл производной

На графике F функции f(x) выбирается точка с абсциссой x0
и вычисляется соответствующая
ордината f(x0).
В окрестности точки x0 выбирается произвольная точка x.
Через точки (x0;f(x0)) и (x;f(x))
на графике F
функции f(x)
проводится секущая
(первая светло-серая линия A5).
Расстояние
Δx = x — x0
устремляется к нулю, в результате секущая переходит в
касательную A
(постепенно темнеющие линии A5 — A1).
Тангенс угла α
между
положительной полуосью и этой касательной A — есть значение производной
функции
в точке
x0.
y= f(x0)+f|(x0)(x- x0) -
уравнение касательной.
Таким образом, tgα= k = f|(x0)
1. Значение производной функции f(x) в точке
xo равно tga — угловому коэффициенту
касательной,
проведенной к графику этой функции в данной точке. Чтобы найти угловой
коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и
ординаты
которых — целые числа. Теперь определим модуль углового коэффициента.
Для этого
построим прямоугольный треугольник ABC, в котором отрезок АВ является гипотенузой.
Важно помнить, что тангенс острого
угла прямоугольного
треугольника — это отношение
противолежащего катета к прилежащему.
Знак производной (углового коэффициента)
можно определить по рисунку,
например, так: если касательная составляет с
положительной полуосью ОХ
острый угол,
то производная положительна,
если касательная составляет с положительной полуосью ОХ тупой угол - отрицательна
(если касательная параллельна оcи OX, то производная равна нулю).


2. Производная непрерывной дифференцируемой функции на
промежутке убывания
(возрастания) не положительна (не отрицательна).

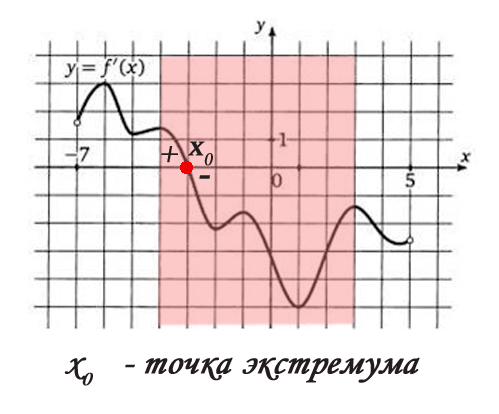
3. Если функция y=f(x) имеет экстремум в точке xo,
то в этой точке производная функции либо
равна нулю, либо не существует.
Заметим, что при переходе через точку максимума изменяется характер монотонности функции:
cлева от точки максимума функция возрастает, справа – убывает. Следовательно, изменяются
знаки
производной: слева от точки максимума производная положительна, справа -
отрицательна.
При переходе через точку минимума также изменяется характер монотонности функции:
слева
от точки минимума функция убывает, справа – возрастает. Следовательно, изменяются знаки
производной: слева от точки минимума производная отрицательна, справа - положительна.
Если же слева и справа от исследуемой точки производная имеет один и тот же знак, то в этой
точке
экстремума нет.
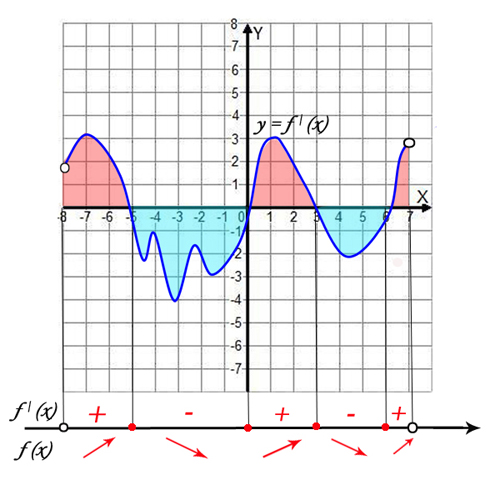
4. Если функция непрерывна на промежутке Х, и
выполняется неравенство f'(x)> o, то
функциия y=f(x)
возрастает на промежутке Х; если же на промежутке Х выполняется
неравенство
f'(x)< o, то функциия y=f(x) убывает на этом промежутке.
Если f'(x)=0
на промежутке Х, то на этом промежутке
функциия y=f(x) постоянна.
Если функция непрерывна не только на промежутке, но и на его концах, то эти
точки
включаются в промежуток монотонности.
|